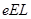问题
计算题
(2011·南通模拟)(18分)如图所示为研究电子枪中电子在电场中运动的简化模型示意图.在xOy平面的第一象限，存在以x轴、y轴及双曲线y=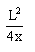
的一段(0≤x≤ L， 0≤y≤ L)为边界的匀强电场区域Ⅰ；在第二象限存在以x＝-L、x＝-2L、y＝0、y＝L的匀强电场区域Ⅱ.两个电场大小均为E，不计电子所受重力，电子的电荷量为e，求：
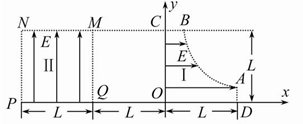
(1)从电场区域Ⅰ的边界B点处由静止释放电子，电子离开MNPQ时的坐标；
(2)由电场区域Ⅰ的AB曲线边界由静止释放电子离开MNPQ的最小动能；
答案
(1) (-2L，0) (2)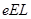
(1)设电子的质量为m，电子在电场Ⅰ中做匀
加速直线运动，出区域Ⅰ时的速度为v0，接着在无电场区域
匀速运动，此后进入电场Ⅱ，在电场Ⅱ中做类平抛运动，假
设电子从NP边射出，出射点纵坐标为y1，
由y=
对于B点y=L，则x=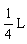
(2分)
所以eE·=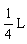 
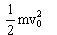(2分)
解得v0=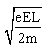 
(1分)
设在电场Ⅱ中运动的时间为t1
L-y1=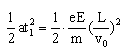
(1分)
解得y1=0，所以原假设成立，即电子离开MNPQ区域的位置坐标为(-2L，0) (2分)
(2)设释放点在电场区域Ⅰ中的坐标为(x，y)，在电场Ⅰ中电子被加速，速度为v1时飞离电场Ⅰ，接着在无电场区域做匀速运动，然后进入电场Ⅱ做类平抛运动，并从NP边离开，运动时间为t2，偏转位移为y2.
eEx=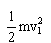
(2分)
y2=
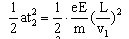(2分)
解得xy2=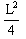
，所以原假设成立，即在电场Ⅰ区域的AB曲线边界由静止释放的所有电子离开MNPQ时都从P点离开的. (2分)
从边界AB出发到P点射出的全过程，由动能定理得：
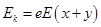
又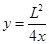
，得到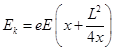
根据数学知识得知，当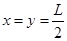
，动能有最小值