问题
解答题
已知(1+x+mx2)10的展开式中x4的系数大于-330,求m的取值范围.
答案
(-∞,-6)∪(-2,+∞)
【思路点拨】遇到三项式先化为二项式,再用二项展开式求解.
解:因为(1+x+mx2)10=[1+x(mx+1)]10
=1+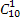 x×(mx+1)+
x×(mx+1)+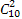 x2(mx+1)2+
x2(mx+1)2+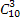 x3(mx+1)3+
x3(mx+1)3+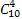 x4(mx+1)4+…+
x4(mx+1)4+…+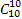 x10(mx+1)10.
x10(mx+1)10.
由此可知,上式中只有第三、四、五项的展开式中含有x4项,其系数分别为: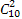 m2,
m2,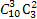 m,
m,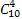 .
.
由已知,得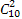 m2+
m2+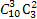 m+
m+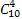 >-330.
>-330.
化简整理,得m2+8m+12>0,即(m+2)(m+6)>0.
所以m>-2或m<-6,故m的取值范围是
(-∞,-6)∪(-2,+∞).
