问题
解答题
将长为64m的绳子剪成两段，每段都围成一个正方形，试问怎样分可使得这两个正方形面积和最小？最小值是多少？
答案
解：设两个正方形边长分别为a，b，则这两个正方形面积之和为a2+b2，
又由完全平方公式，可得a2+b2=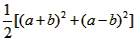
，
∴
，
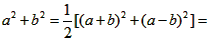
答：这两个正方形面积和的最小值为128m2。
搜题请搜索小程序“爱下问搜题”
将长为64m的绳子剪成两段，每段都围成一个正方形，试问怎样分可使得这两个正方形面积和最小？最小值是多少？
解：设两个正方形边长分别为a，b，则这两个正方形面积之和为a2+b2，
又由完全平方公式，可得a2+b2=，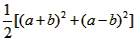
∴，
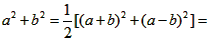
答：这两个正方形面积和的最小值为128m2。