问题
计算题
如图所示，有一磁感强度B=9.1×10-4T的匀强磁场，C、D为垂直于磁场方向的同一平面内的两点，它们之间的距离L=0.05m，今有一电子在此磁场中运动，它经过C点的速度v的方向和磁场垂直，且与CD之间的夹角θ=30°。（电子的质量m==9.1×10-31kg，电量e==1.6×10-19C）
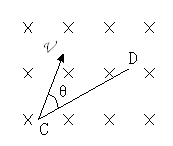
（1）若此电子在运动后来又经过D点，则它的速度应是多大？
（2）电子从C点到D点所用的时间是多少？
答案
（1）8×106m/s（2）6.5×10-9
题目分析：（1）根据题意做出电子在磁场中作匀速圆周运动轨迹，如图所示
由平面几何知识得，电子运动半径的大小为
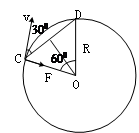
R=L ① （2分）
而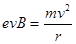
② （1分）
由①②得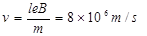 
（1分）
（2）电子在磁场中从C点到D点的圆弧所对的圆心角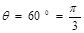
（1分）
而电子运动的周期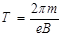 
（1分）
所以电子从C点到D点所用时间为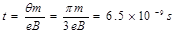 
（2分）
点评：本题难度中等，求解粒子在匀强磁场中的运动问题，注意是利用洛仑兹力提供向心力而做圆周运动的结论，判断出粒子的大概运动轨迹，运动时间由圆心角的大小决定，其中考查了学生利用几何知识的能力