问题
填空题
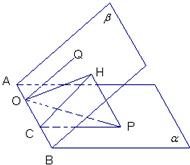
已知点O在二面角α-AB-β的棱上,点P在α内,且∠POB=45°.若对于β内异于O的任意一点Q,都有∠POQ≥45°,则二面角α-AB-β的取值范围是______.
答案
若二面角α-AB-β的大小为锐角,
则过点P向平面β作垂线,设垂足为H.
过H作AB的垂线交于C,
连PC、CH、OH,则∠PCH就是所求二面角的平面角.
根据题意得∠POH≥450,
由于对于β内异于O的任意一点Q,都有∠POQ≥45°,
∴∠POH≥45°,
设PO=2x,则PH≥
x2
又∵∠POB=45°,
∴OC=PC=
x,而在Rt△PCH中应有2
PC>PH,
∴显然矛盾,故二面角α-AB-β的大小不可能为锐角.
即二面角α-AB-β的范围是:[90°,180°].
若二面角α-AB-β的大小为直角或钝角,
则由于∠POB=45°,
结合图形容易判断对于β内异于O的任意一点Q,都有∠POQ≥45°.
即二面角α-AB-β的范围是[90°,180°].
故答案为:[90°,180°].