在PC上任取一点D并作PO⊥平面APB，则∠DPO就是直线PC与平面PAB所成的角．         

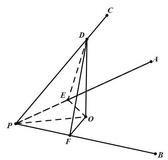
过点O作OE⊥PA，OF⊥PB，因为DO⊥平面APB，则DE⊥PA，DF⊥PB．

△DEP≌△DFP，∴EP=FP，∴△OEP≌△OFP，

因为∠APC=∠BPC=60°，所以点O在∠APB的平分线上，即∠OPE=30°．

设PE=1，∵∠OPE=30°∴OP=

在直角△PED中，∠DPE=60°，PE=1，则PD=2．

在直角△DOP中，OP=

即直线PC与平面PAB所成角的余弦值是