问题
计算题
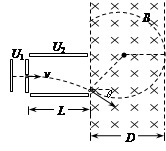
（18分）如图17所示，一带电微粒质量为m=2.0×10-11kg、电荷量为q=+1.0×10-5C，从静止开始经电压为U1=100V的电场加速后，水平进入两平行金属板间的偏转电场中，偏转电压为U2=100V，接着进入一个方向垂直纸面向里、宽度为D=34.6cm的匀强磁场区域。已知偏转电场中金属板长L=20cm，两板间距d =17.3cm,带电微粒的重力忽略不计。求：
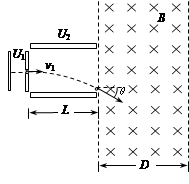
（1）带电微粒进入偏转电场时的速率v1；
（2）带电微粒射出偏转电场时的速度偏转角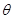
；
（3）为使带电微粒不会从磁场右边界射出，该匀强磁场的磁感应强度的最小值B。
答案
（1）
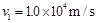（2）
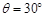（3）B=0.1T
（19分）（1）带电微粒经加速电场加速后速度为v1，根据动能定理
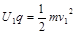
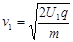
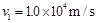（3分）
（2）带电微粒在偏转电场中只受电场力作用，做类平抛运动。
在水平方向：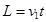 
带电微粒在竖直方向做匀加速直线运动，加速度为a，出电场时竖直方向速度为v2，
竖直方向：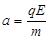 
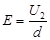
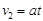
由几何关系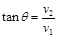 
联立求解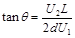 
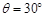（3分）
（3）带电微粒进入磁场做匀速圆周运动，洛伦兹力提供向心力，设微粒轨道半径为R，由几何关系知：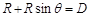
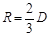
设微粒进入磁场时的速度为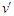
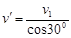
由牛顿运动定律及运动学规律
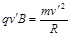
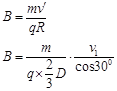
B=0.1T （3分）
若带电粒子不射出磁场，磁感应强度B至少为0.1T。
本题考查的是带电粒子在电场和磁场中运动与力学综合的相关问题，首先根据动能定理可解出速率；再根据电场力提供加速度可解得偏转角；根据洛伦兹力提供圆周运动的向心力利用牛顿运动定律及运动学规律可解出结果；