问题
问答题
已知非齐次线性方程组
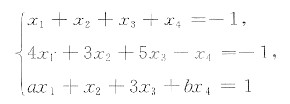
有3个线性无关的解．
(1) 证明方程组系数矩阵A有秩r(A)=2．
(2) 求a，b的值及方程组的通解．
答案
参考答案：(1) 用线性相关性判断秩的方法．
依题意，设α1，α2，α3是非齐次方程组的3个线性无关的解，则α1-α2，α1-α3是Ax=0线性无关的解．所以
n-r(A)≥2，即r(A)≤2．
又矩阵A中有二阶子式不为0，于是r(A)≥2，所以秩r(A)=2．
(2) 对增广矩阵作初等行变换，有
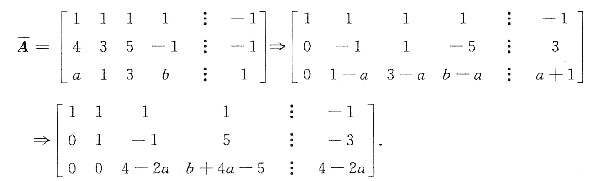
由r(A)=r
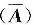=2(已证)
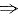a=2，b=-3．
又α=(2，-3，0，0)T是原方程组的解，η1=(-2，1，1，0)T．η2=(4，-5，0，1)是AX=0的基础解系，所以原方程组的通解是
α+K1η1+K2η2(K1，K2为任意常数)．
解析：[考点提示] 向量组的线性相关性、增广矩阵、线性方程组的通解．
