问题
问答题
已知平面上三条不同直线的方程分别为
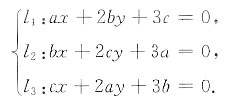
试证这三条直线交于一点的充分必要条件为a+b+c=0.
答案
参考答案:由题设,三条直线交于一点等价于线性非齐次方程组

有唯一解.下面先证必要性,设系数矩阵为A,增广矩阵为B,则
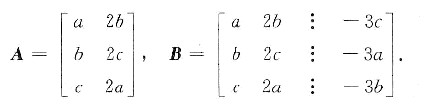
方程组①有唯一解,则r(A)=r(B)=2,因而|B|=0,即
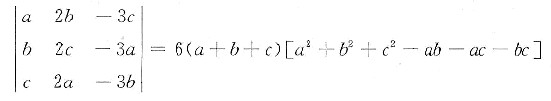
=3(a+b+c)r(a-b)2+(b-c)2+(c-a)2]=0.
由已知3条直线不相同,从而
(a-b)2+(b-c)2+(c-a)2≠0,
因此a+b+c=0.至此,必要性得证.
再证充分性,由于a+b+c=0,则|B|=0,因此,r(B)≤2.又因为
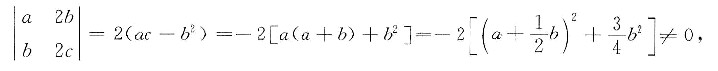
由此r(A)=2,所以r(A)=r(B)=2,则方程组①有唯一解,也即三条直线交于一点.充分性得证.
解析:[考点提示] 线性非齐次代数方程组.
注 本题的另外一种证法是:
(1) 必要性:设三条直线交于一点(x0,y0),则[*]是Ax=0的非零解,其中
[*]
因此|A|=0,即
|A|=-3(a+b+c)[(a-b)2+(b-c)2+(c-a)2].
由于(a-b)2+(b-c)2+(c-a)2≠0,知a+b+c=0.
(2) 充分性:由方程组[*]的三个方程相加,并结合a+b+c=0,知上述方程等价于以下方程组
[*]
由于
[*]
=[a2+2ab+b2+a2+b2]=-[(a+b)2+a2+b2]≠0.
因此原方程组解唯一,从而三条直线交于一点.
