问题
解答题
设有编号为1，2，3，4，5的五个球和编号为1，2，3，4，5的五个盒子，现将这五个球放入5个盒子内，
（1）只有一个盒子空着，共有多少种投放方法？
（2）没有一个盒子空着，但球的编号与盒子编号不全相同，有多少种投放方法？
答案
解：（1）只有一个盒子空着，则有且只有一个盒子中投放两个球，另外3只盒子中各投放一个球，
先将球分成2，1，1，1的四组，共有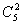
种分法，
再投放到五个盒子的其中四个盒子中，共有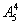
种放法，
所以，满足条件的投放方法共有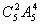
=1200（种）；
（2）五个球投放到五个盒子中，每个盒子中只有一个球，共有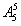
种投放方法，
而球的编号与盒子编号全相同的情况只有一种，
所以，球的编号与盒子编号不全相同的投放方法共有
-1=119（种）．