问题
填空题
等腰直角三角形ABC的斜边AB在平面α内,若AC与α所成角为30°,则斜边上的中线CM与α所成的角为______.
答案
设AC=a,因为三角形ABC等腰直角三角形,所以AB=
a,2
因为CM是斜边上的中线,
所以CM=
.
a2 2
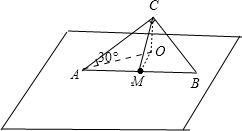
过点C作CO⊥α,交α于点O,连接OA,OM,所以OC⊥OA,OC⊥OM,
所以AC与α所成角为∠CAO并且等于30°,MC与α所成角为∠CMO.
因为在△ACO中,AC=a,∠CAO=30°,OC⊥OA,
所以OC=
.a 2
又因为在△COM中有OC⊥OM,CM=
,
a2 2
所以sin∠CMO=
=OC CM
=a 2
a2 2
,2 2
所以∠CMO=45°.
故答案为:45°.
