问题
问答题
已知α1,α2,α3,α4是线性方程组Ax=0的一个基础解系.若β1=α1+tα2,β2=α2+tα3,β3=α3+tα4,β4=α4+tα1.讨论实数t满足什么关系时,β1,β2,β3,β4也是Ax=0的一个基础解系.
答案
参考答案:本题考查一个向量组成其为一个线性方程组的基础解系的充分必要条件,即该向量组的所有向量线性无关,且都是原方程组的解;同时该向量组中向量的个数等于原方程组的解空间的维数.由题设,α1,α2,α3,α4是Ax=0的基础解系,则Ax=0的解空间维数是4,又β1,β2,β3,β4都是α1,α2,α3,α4的线性组合,所以β1,β2,β3,β4都是Ax=0的解.至此只需‘讨论β1,β2,β3,β4是否线性无关即可.
设 k1β1+k2β2+k3β3+k4β4=0. ①
将题设中βi的表达式代入①式,并化简得
(k1+tk4)α1+(k2+tk1)α2+(k3+tk2)α3+(k4+tk3)α4=0.
已知α1,α2,α3,α4线性无关,因此有
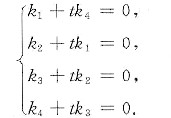
记方程组②的系数行列式为|B|,则

因此β1,β2,β3,β4为Ax=0的一个基础解系的充要条件是β1,β2,β3,β4线性无关,也即②只有零解,即|B|≠0.所以当1-t4≠0,即t≠±1时满足条件.
解析:[考点提示] 基础解系.
注 在分析β1,β2,β3,β4是否线性无关时,也可利用β1,β2,β3,β4与α1,α2,α3,α4之间的关系:
[*]
直接得出β1,β2,β3,β4线性无关的充要条件是
[*]
