问题
填空题
（理）已知圆柱的体积是
|
答案
∵V圆柱=πr2h=πh=
π，∴h=6 6
过A向底面作垂线，垂足必落在底面圆周上，设为
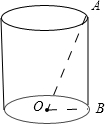
B，则∠AOB为所求
在Rt△AOB中，tan∠AOB=
=|AB| |OB|
=6 1 6
∴∠AOB=arctan6
故答案为arctan6
搜题请搜索小程序“爱下问搜题”
（理）已知圆柱的体积是
|
∵V圆柱=πr2h=πh=
π，∴h=6 6
过A向底面作垂线，垂足必落在底面圆周上，设为
B，则∠AOB为所求
在Rt△AOB中，tan∠AOB=
=|AB| |OB|
=6 1 6
∴∠AOB=arctan6
故答案为arctan6