问题
解答题
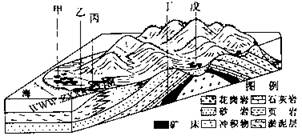
（文）如图，在矩形ABCD中，AB=3
（1）求证：BC'⊥面ADC'； （2）求二面角A-BC'-D的正弦值； （3）求直线AB和平面BC'D所成的角的正弦值． |
答案
（1）
DA⊂平面ABD AB是BC′在平面ABD内的射影 DA⊥AB
⇒
⇒BC′⊥平面ADC′…（4分）DA⊥BC′ BC′⊥DC′ DA∩DC′=D
（2）BC′⊥平面ADC′，C′D⊂平面ADC′，C′A⊂平面ADC′，
所以BC′⊥C′D，BC′⊥C′A，
所以∠DC′A是二面角A-BC′-D的平面角，…（6分）
而
⇒DA⊥面ABC′⇒DA⊥AC′…（7分）BC′⊥平面ADC′⇒DA⊥BC′ DA⊥AB BC′∩AB=B
在Rt△AC′D中，sin∠DC′A=
=DA C′D
=3 3 3
．…（8分）3 3
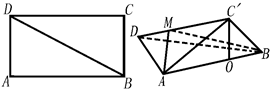
（3）作AM⊥DC′于M，连接BM，
BC′⊥C′A，AM∩AC′=A，∴BC′⊥平面ADC′
BC′⊂平面SDC′，∴平面ADC′⊥平面BDC′，
又AM⊥DC′，DC′=平面ADC′∩平面BDC′，
所以AM⊥平面BC′D，
所以∠ABM是AB与平面BC′D所成的角…（10分）
在Rt△DAC′中，AM•DC′=AD•AC′，AM=
=AD•AC′ DC′
=3•3 2 3 3
…（12分）6
在Rt△ABM中，sin∠ABM=
=AM AB
=6 3 3
（13分）2 3
+4H++3e-=NO+2H2O 。 已知Cu2O能使上述还原过程发生。
_。