问题
问答题
在椭圆
=1的第一象限部分上求一点P，使该点处的切线、椭圆及两坐标轴所围图形面积为最小(其中a＞0，b＞0)．
答案
参考答案：先求出切线及与坐标轴的交点，所围图形的面积是动点(x0，y0)的函数，再由此确定x0，y0．
设P(x0，y0)为所求点，则此点处椭圆的切线方程为
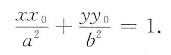
令x=0，得该切线在y轴上的截距为
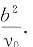
令y=0，得该切线在x轴上的截距为
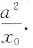
于是所围图形的面积为
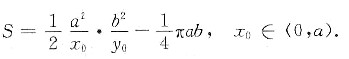
设S1=x0y0=
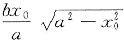，因为S1的极大值点即S的极小值点，为计算方便，将求S的极小值点改求S1的极大值点．
今S’1=0．解得在(0，a)内的唯一驻点x0=
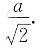
由S’1在点x0=
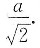处的左侧为正，右侧为负，知x0=
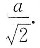为S1的极大值点，即S的极小值点．所以当x0=
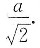时，S为最小．此时y0=
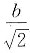，即P
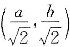为所求点．
解析：[考点提示] 函数极值的综合题．