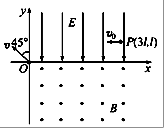
如图所示,在平面直角坐标系xOy内,第Ⅰ象限有沿-y方向的匀强电场,第Ⅳ象限有垂直于纸面向外的匀强磁场.现有一质量为m、带电量为+q的粒子(重力不计)以初速度v0沿-x方向从坐标为(3l,l)的P点开始运动,接着进入磁场后由坐标原点O射出,射出时速度方向与y轴方向夹角为45°,求:
(1)粒子从O点射出时的速度v;
(2)电场强度E的大小;
(3)粒子从P点运动到O点所用的时间.
(1) v=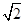 v0 (2) E=
v0 (2) E=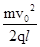 (3) T=t1+t2=(2+
(3) T=t1+t2=(2+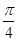 )
)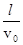
题目分析:(1)带电粒子在电场中做类平抛运动,进入磁场后做匀速圆周运动,最终由O点射出.(如图)
根据对称性可知,粒子在Q点时的速度大小与粒子在O点的速度大小相等,均为v,方向与-x轴方向成45°角,则有
vcos45°=v0 (2分) 解得v=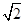 v0
v0
(2)在P到Q过程中,由动能定理得
qEl=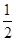 mv2-
mv2-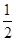 m
m 解得E=
解得E=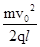
(3)设粒子在电场中运动的时间为t1,则l=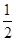 a
a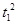 =
=
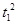
设粒子在磁场中做匀速圆周运动的半径为r,由几何关系得
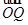 =3l-v0t1
=3l-v0t1 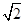 r=
r=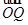
粒子在磁场中的运动时间为 t2= ×
×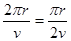
由以上各式联立求得粒子在由P到O过程中的总时间为T=t1+t2=(2+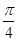 )
)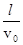
点评:带电粒子在电场中的运动,综合了静电场和力学的知识,分析方法和力学的分析方法基本相同.先分析受力情况再分析运动状态和运动过程,然后选用恰当的规律解题.解决这类问题的基本方法有两种,第一种利用力和运动的观点,选用牛顿第二定律和运动学公式求解;第二种利用能量转化的观点,选用动能定理和功能关系求解.
