设AB=1，作AO⊥BC于点O，连DO，以点O为原点，OD，OC，OA的方向分别为x轴、y轴、z轴方向，建立坐标系，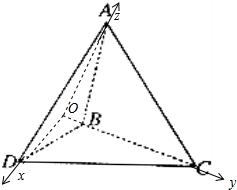

得下列坐标：

O（0，0，0），D（

3

2

，0，0），B（0，

1

2

，0），C（0，

3

2

，0），

A（0，0，

3

2

）

∴

AB

=（0，

1

2

，-

3

2

），

AD

=(

3

2

，0，-

3

2

)，

AC

=(0，

3

2

，-

3

2

)

设平面ADC的法向量为

n

=(x，y，z)，则

3 x 2 - 3 2 z=0 3 2 y- 3 2 z=0

∴可取

n

=(

3

，1，

3

)

∴AB与平面ADC所成角的正弦值为|cos＜

n

，

AB

＞|=|

n • AB

| n || AB |

|=|

1 2 - 3 2

1× 7

|=

7

7

故答案为：

7

7