问题
解答题
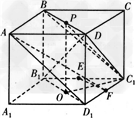
已知单位正方体ABCD-A1B1C1D1,E、F分别是棱B1C1和C1D1的中点,试求:
(1)AD1与EF所成角的大小;
(2)AF与平面BEB1所成角的余弦值;
(3)二面角C1-DB-B1的正切值.
答案
解法一:(1)如图,连结B1D1,
∵E、F分别是B1C1和C1D1的中点,
∴EF∥B1D1,
则AD1与EF所成的角等于AD1与B1D1所成的角,∠AD1B1即为所求,
由正方体的性质得△AD1B1为等边三角形,
∴∠AD1B1=60°,
故AD1与EF所成角的大小为60°.
(2)∵平面AA1D1D∥平面BEB1,
∴AF与平面BEB1所成的角等于AF与平面AA1D1D所成的角,
又AF与平面AA1D1D所成的角为∠FAD1,
在△FAD1中,AD1=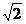 ,FD1=
,FD1= ,FA=
,FA=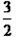 ,
,
∴ cos∠FAD1=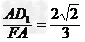
(3)取B1D1中点O,BD中点P,连结C1O,C1P,OP,则OP⊥BD,C1P⊥BD,
∴∠C1PO为二面角C1-DB-B1的平面角.
在Rt△OPC1中,C1O=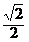 ,OP =1,
,OP =1,
:. tan ∠C1PO =