搜题请搜索小程序“爱下问搜题”
问题 填空题
正四棱柱ABCD-A1B1C1D1的底面长为
2
，侧棱长为1，则这个棱柱的侧面对角线AB1与BC1所成角的余弦值等于______．
答案

如图，

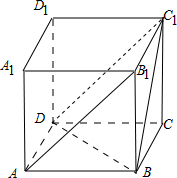
连结DC1，在正四棱柱ABCD-A1B1C1D1中，由AD∥B1C1，AD=B1C1，

所以四边形ADC1B1为平行四边形，则∠DC1B对角线AB1与BC1所成角．

由题意求得DC1=BC1=

3
，DB=2．

所以cos∠DC1B=

DC12+BC12-DB2
2DC1•BC1
=
(
3
)2+(
3
)2-22
2×
3
×
3
=
1
3
．

故答案为

1
3

材料分析题

    俄罗斯小朋友叶廖莎向小亮介绍自己的国家：“请让我用刚学到的中文向你介绍我的祖国。莫斯科是我的首都，是全国最大的城市，这里有克里姆林宫、红场等名胜古迹。圣彼得堡是全国最大的海港和第二大城市。在北冰洋沿岸，有我国唯一的不冻港摩尔曼斯克，这里可以看到极昼现象。对了，太平洋沿岸的符拉迪沃斯托克是我国离北京最近的海港。听说你很想了解俄罗斯，你知道吗？20世纪世界上第一颗人造地球卫星、第一艘载人宇宙飞船、第一座核电站和第一颗轻弹都诞生在我们的国家……”

做一做：

（1）把叶廖莎信中介绍的城市或海港和下图中代表它们的数码一一对应。

（2）叶廖莎信中反映，俄罗斯居世界领先水平的工业部门有哪些？

    _________________________________________________________________________________________

（3）请你写一封信，把自己家乡介绍给叶廖莎。

    _________________________________________________________________________________________

    _________________________________________________________________________________________
查看答案
问答题 简答题

什么是渠道水力最优断面？
查看答案