问题
选择题
在空间四边形ABCD中,AD=BC=2,E、F分别是AB、CD的中点,EF=
|
答案
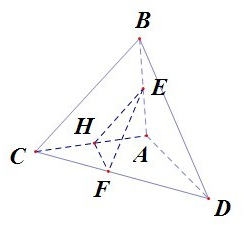
取AC的中点H,连结HE,HF,EF,
因为E、F分别是AB、CD的中点,
所以HF∥BC,HF=
BC=1,1 2
HF∥AD,HF=
AD=1,1 2
所以HE与HF所成的角即为AD与BC所成的角.
在三角形EFH中,HF=1,HE=1,EF=
,2
所以三角形EHF为直角三角形,所以HE⊥HF,
即AD与BC所成角的大小为90°.
故选D.
