问题
问答题
设有一根长为a的铁丝，将其分成两段，分别围成圆形和正方形，如果设所围圆形的面积为S1，正方形的面积为S2，证明：当
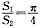时，S1+S2的值最小。
答案
参考答案：[证明] 将铁丝分为两段，设长分别为x，a-x。
将长为x的部分构成半径为R的圆形，则2πR-x，从而[*]，故
[*]
求导数，得
[*]
令S"=0可求得S的唯一驻点
[*]
又[*]，可知[*]为s的极小值点。
由于实际问题存在最小值，可知[*]为S的最小值点。
当[*]时，由
[*]
可知[*]。因此，[*]时，S1+S2的值最小。