问题
解答题
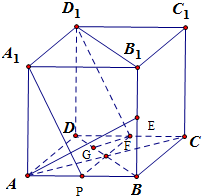
在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(1)证明:BC⊥AE
(2)求AE与D1F所成的角;
(3)设AA1=1,求点F到平面DBB1D1 的距离.
答案
(1)∵正方体ABCD-A1B1C1D1,∴BC⊥平面AA1B1B,
∵AE⊂平面AA1B1B,∴BC⊥AE
(2)取AB的中点P,并连结A1P,EP
正方形AA1B1B中,可得△A1AP≌△ABE,
∴A1P⊥AE,
∵AD
A1D1∥ .
PF,∥ .
∴四边形A1D1FP是平行四边形,可得A1P∥D1F
即AE⊥D1F,所以AE与D1F所成的角为90°
(3)过F作FG⊥BD于G,
∵BB1⊥平面ABCD,FG⊂平面ABCD,
∴BB1⊥FG
∵FG⊥BD,BD∩BB1=B,
∴FG⊥平面DBB1D1,可得F到平面DBB1D1的距离是FG的长度,
∵正方形ABCD中,FG的长度等于CA长度的1 4
∴F到平面DBB1D1 的距离等于
AC=1 4 2 4
