问题
填空题
正方体ABCD-A1B1C1D1中,E,F分别是正方形ADD1A1和ABCD的中心,G是CC1的中点,设GF,C1E与AB所成的角分别为α,β,则α+β=______.
答案
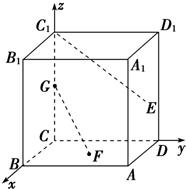
建立坐标系如图,
B(2,0,0),A(2,2,0),G(0,0,1),F(1,1,0),C1(0,0,2),E(1,2,1).
则
=(0,2,0),BA
=(1,1,-1),GF
=(1,2,-1),C1E
∴cos<
,BA
>=GF
=
•BA GF |
|×| BA
|GF
=2 2× 3
,1 3
同理cos<
,BA
>=C1E
,2 3
∴cosα=
,sinα=1 3
,2 3
cosβ=
,sinβ=2 3
,1 3
∴cos(α+β)=cosαcosβ-sinαsinβ=
•1 3
-2 3
•2 3
=01 3
∴α+β=90°,
故答案为:90°.
