问题
选择题
| 将正方形ABCD沿对角线BD折成直二面角A-BD-C,有如下四个结论: ①AC⊥BD;②△ACD是等边三角形;③AB与平面BCD所成的角为60°;④AB与CD所成的角为60°. 其中错误的结论是( )
|
答案
解:取BD的中点E,则AE⊥BD,CE⊥BD.
∴BD⊥面AEC.
∴BD⊥AC,故①正确.
设正方形边长为a,则AD=DC=a,AE= 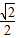 a=EC.
a=EC.
∴AC=a.
∴△ACD为等边三角形,故②正确.
∠ABD为AB与面BCD所成的角为45°,故③不正确.
以E为坐标原点,EC、ED、EA分别为x,y,z轴建立直角坐标系,
则A(0,0, 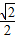 a),B(0,-
a),B(0,- 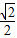 a,0),D(0,
a,0),D(0, 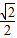 a,0),C(
a,0),C( 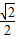 a,0,0).
a,0,0).
AB =(0,- 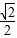 a,-
a,-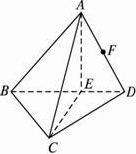 a), DC =(
a), DC =( 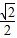 a,-
a,-  a,0).
a,0).

∴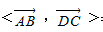 =60°
=60°
故④正确.
故选C

