阅读下面一段文言文,完成下面问题。
吴起传
吴起者,卫人也,好用兵。齐人攻鲁,鲁欲将吴起,吴起取齐女为妻,而鲁疑之。吴起于是欲就名,遂杀其妻,以明不与齐也。鲁卒以为将。将而攻齐,大破之。鲁人或恶吴起曰:“起之为人,猜忍人也。其少时,乡党笑之,吴起杀其谤己者三十余人。鲁君疑之,起杀妻以求将。夫鲁小国,而有战胜之名,则诸侯图鲁矣。且鲁、卫兄弟之国也,而君用起,则是弃卫。”鲁君疑之,谢吴起。
吴起于是闻魏文侯贤,欲事之。文侯问李克曰:“吴起何如人哉?”李克曰:“起贪而好色,然用兵,司马穰苴不能过也。”魏文侯以为将,击秦,拔五城。起之为将,卧不设席,行不骑乘,与士卒分劳苦。文侯以吴起善用兵。乃以为西河守,以拒秦、韩。魏文侯既卒,起事其子武侯。武侯浮西河而下,中流,顾而谓吴起曰:“美哉乎山河之固,此魏国之宝也!”起对曰:“在德不在险。若君不修德,舟中之人尽为敌国也。”武侯曰:“善。”田文既死,公叔为相,尚魏公主,而害吴起。因与武侯言曰:“夫吴起贤人也。臣窃恐起之无留心也。试延以公主,以此卜之。吴起辞魏武侯。武侯疑之而弗信也。吴起惧得罪,遂去,即之楚。
楚悼王素闻起贤,至则相楚,明法审令,捐不急之官,废公族疏远者,以抚养战斗之士。要在强兵,破驰说之言从横者。故楚之贵戚尽欲害吴起。及悼王死,宗室大臣作乱而攻吴起,吴起走之王尸而伏之。击起之徒因射刺吴起,并中悼王。
太史公曰:世俗所称师旅,皆道吴起《兵法》,世多有,故弗论,论其行事所施设者,语曰:“能行之者未必能言,能言之者未必能行”。吴起说武侯以形势不如德,然行之于楚,以刻暴少恩亡其躯。悲夫! ——(选自《史记·吴起列传》)
1、对下列句子中加粗词语的解释,不正确的一项是( )
A、鲁君疑之,谢吴起 谢:道歉
B、起事其子武侯 事:侍奉
C、公叔为相,尚魏公主 尚:臣娶君女
D、明法审令,捐不急之官 捐:撤除
2、下列各组句子中,分别表明吴起“善用兵”和“刻暴少恩”的一组是( )
A、 ①将而攻齐,大破之 ②遂杀其妻,以明不与齐也
B、 ①卧不设席,行不骑乘 ②吴起于是闻魏文侯贤,欲事之
C、 ①以为将,击秦,拔五城 ②吴起惧得罪,遂去,即之楚
D、 ①吴起说武侯以形势不如德 ②捐不急之官,废公族疏远者
3、下列对原文有关内容的分析和概括,不正确的一项是( )
A、齐国进攻鲁国时,鲁国想用吴起做 * * ,又因吴起娶了齐国女子为妻而猜疑他。
B、魏文侯听说吴起贤明,又很有军事才能,就重用吴起为 * * ,让他率军进攻秦国,夺取了五座城池。
C、公叔做宰相时,忌妒吴起,就向魏武侯进谗言,吴起害怕获罪,就离开魏国,马上到楚国去了。
D、吴起在楚国担任相职,申明法度,赏罚分明,裁减闲职,废除部分贵族爵位,触犯了王室大臣的利益,终于在楚悼王死后招致杀身之祸。
4.把文中画线的句子翻译成现代汉语。
(1)吴起于是欲就名,遂杀其妻,以明不与齐也。
______________________________________________________
(2)试延以公主,以此卜之。
______________________________________________________
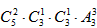 =540个,
=540个, =720个,
=720个, =360(个),
=360(个), =300(个),
=300(个),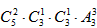 =540个,
=540个, =720个,
=720个, =360(个),
=360(个), =300(个),
=300(个),