问题
选择题
在正方体ABCDA1B1C1D1中,M为DD1的中点,O为四边形ABCD的中心,P为棱A1B1上任一点,则异面直线OP与MA所成的角为( )
A.30°
B.45°
C.60°
D.90°
答案
∵A1B1⊥面ADD1A1,AM?面ADD1A1,
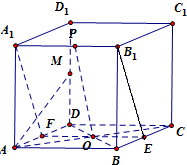
∴A1B1⊥AM.
设点O与A1B1确定的平面为α,α∩AD=F且α∩BC=E,则F、E为AD、BC的中点,
根据正方形的性质,可得AM⊥A1F.
∵A1F∩A1B1=A1,A1F、A1B1?平面面A1FEB1,∴AM⊥面A1FEB1,
又∵OP?面A1FEB1,∴AM⊥OP.
即直线OP与直线AM所成的角是90°.
故选:D
