问题
选择题
三棱锥A-BCD的棱长全相等,E是AD中点,则直线CE与直线BD所成角的余弦值为( )
|
答案
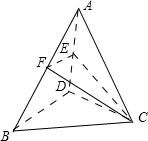
如图,取AB中点F,连接EF,因为E、F分别为AD、AB的中点,则EF为三角形ABD的中位线,所以EF∥BD,
所以直线EF与CE所成的角即为直线CE与直线BD所成角,
因为三棱锥A-BCD的棱长全相等,设棱长为2a,则EF=a,
在等边三角形ABC中,因为F为AB的中点,所以CF为边AB上的高,
所以CF=
=BC2-BF2
=(2a)2-a2
a,3
则CE=CF=
a,3
在三角形CEF中,cos∠CEF=
=CE2+EF2-CF2 2CE•EF
=a2 2a•
a3
.3 6
所以,直线CE与直线BD所成角的余弦值为
.3 6
故选A.
