问题
填空题
空间四边形ABCD中,对角线BD=12
|
答案
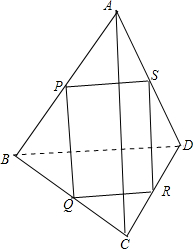
连接P,Q,因为PQ是△ABC的中位线,所以PQ∥AC,且PQ=
AC.1 2
同理,SR∥AC,PQ∥BD,且SR=
AC=21 2
,PS=2
BD=61 2
.2
所以四边形PQRS边形,∠SPQ或其补角即为AC与BD所成的角.
∵sPQRS=PS?PQ?sin∠SPQ?sin∠SPQ=
=SPQRS PS?PQ
.3 2
∴∠SPQ=60°或120°.
所以AC与BD所成角的大小为60°.
故答案为:60°.
