问题
选择题
空间四边形ABCD角线与四边都相等,E为AD的中点,则AB与CE所成的角是( )
|
答案
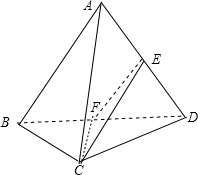
取BD中点F,连接EF,CF,
则EF∥AB,
∠FEC(或其补角)即为AB与CE所成的角.
因为 空间四边形ABCD各边及对角线AC BD都等,设他们的长度都为2a;
所以:CE=CF=
•2a=3 2
a,EF=a;3
根据余弦定理可得:cos∠CEF=
=EF2+CE2-CF 2 2EF•EC
=a2+(
a)2-(3
a)23 2•
a• a3
.3 6
所以:∠FEC=arccos
.3 6
即AB与CE所成的角是arccos
.3 6
故选:B.
