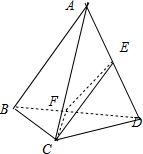
如图所示，取BD的中点F，连接EF，CF，

则EF与CE所成的角即为异面直线AB与CE所成角，

设正四面体ABCD的棱长为2a，（a＞0），

则EF=

1

2

AB=a，CE=CF=2a•sin60°=

3

a，

故在△CEF中，cos∠CEF=

CE2+EF2-CF2

2×CE×EF

=

( 3 a)2+a2-( 3 a)2

2× 3 a×a

=

3

6

，

故∠CEF=arccos

3

6

故答案为：arccos

3

6