(16分) 如图所示,在xoy坐标平面的第一象限内有一沿y轴负方向的匀强电场,在第四象限内有一垂直于平面向里的匀强磁场。现有一质量为m、电量为+q的粒子(重力不计)从坐标原点O以速度大小为v0射入磁场,其入射方向与x轴的正方向成30°角。当粒子第一次进入电场后,运动到电场中P点处时,方向与x轴正方向相同,P点坐标为〔( )L,L〕。(sin37°=0.6,cos37°=0.8)求:
)L,L〕。(sin37°=0.6,cos37°=0.8)求:
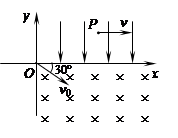
(1)粒子运动到P点时速度的大小为v;
(2)匀强电场的电场强度E和匀强磁场的磁感应强度B;
(3)粒子从O点运动到P点所用的时间t。
(1) (2)
(2)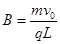 (3)
(3)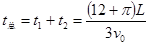
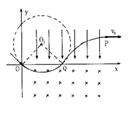
题目分析:(1)粒子运动轨迹如图所示,OQ段为圆周,QP段为抛物线,粒子在Q点时的速度
大小为v0,根据对称性可知,方向与x轴正方向成30°角,可得:
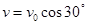 (2分)
(2分)
解得: (1分)
(1分)
(2)在粒子从Q运动到P的过程中,由动能定理得
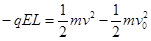 2分)
2分)
解得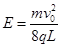 (1分)
(1分)
水平方向的位移为 (1分)
(1分)
竖直方向的位移为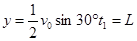 (1分)
(1分)
可得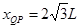
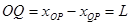 (1分)
(1分)
由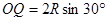 ,故粒子在OQ段圆周运动的半径
,故粒子在OQ段圆周运动的半径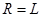 (1分)
(1分)
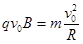 (2分)
(2分)
解得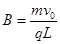 (1分)
(1分)
(3)粒子从O点运动到Q所用的时间为: (1分)
(1分)
设粒子从Q到P所用时间为t2,在竖直方向上有 (1分)
(1分)
则粒子从D点运动到P点所用的时间为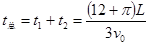 (1分)
(1分)
点评:难度较大,粒子在交替复合场中的运动,首先分析粒子的受力情况,把整体的运动分解为几个分段运动,判断运动轨迹,由类平抛运动和圆周运动进行分析求解
