解：取CD的中点为N，连接BN，

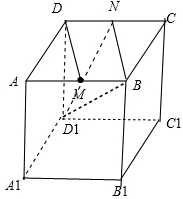
因为在正方体ABCD-A₁B₁C₁D₁中，M为棱AB的中点，

所以DM∥BN，所以异面直线DM与D₁B所成角等于直线BN与D₁B所成角．

设正方体的棱长为2，

所以D₁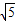N= ，BN= 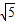，D₁B=2  ，

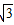所以在△D₁BN中，由余弦定理可得：cos∠D₁BN= ．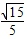

故选B．