答案：C

专题：计算题．

分析：本题考查的知识点是线面夹角，由已知中侧棱垂直于底面，我们过D点做BC的垂线，垂足为E，则DE⊥底面ABC，且E为BC中点，则E为A点在平面BB₁C₁C上投影，则∠ADE即为所求线面夹角，解三角形即可求解．

解答：解：如图，

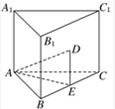
取BC中点E，连接DE、AE、AD，

依题意知三棱柱为正三棱柱，

易得AE⊥平面BB₁C₁C，故∠ADE为AD与平面BB₁C₁C所成的角．

设各棱长为1，则AE=  ，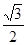

DE=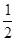 ，tan∠ADE= ，

∴∠ADE=60°．

故选C

点评：求直线和平面所成的角时，应注意的问题是：（1）先判断直线和平面的位置关系．（2）当直线和平面斜交时，常用以下步骤：①构造--作出或找到斜线与射影所成的角；②设定--论证所作或找到的角为所求的角；③计算--常用解三角形的方法求角；④结论--点明斜线和平面所成的角的值．