问题
选择题
已知在四面体ABCD中，E、F分别是AC、BD的中点，若CD=2AB=4，EF⊥AB，则EF与CD所成的角为（ ）
|
答案
解：设G为AD的中点，连接GF，GE，则GF，GE分别为△ABD，△ACD的中线．
∴GF∥AB，且GF=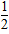
AB=1，GE∥CD，
且GE=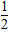
CD=2，
则EF与CD所成角的度数等于EF与GE所成角的度数又EF⊥AB，GF∥AB，
∴EF⊥GF 则△GEF为直角三角形，GF=1，GE=2，∠GFE=90°
∴在直角△GEF中，sin∠GEF=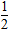
∴∠GEF=30°．
故选D．
