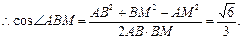（1）∵∠BAC=∠CAD=∠DAB=60°， AC=AD=2，AB=3， ∴△ABC≌△ABD，BC=BD.取CD的中点M，连AM、BM，则CD⊥AM，CD⊥BM. ∴CD⊥平面ABM，于是AB⊥BD.

（2）过A作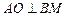于O，∵CD⊥平面ABM，∴CD⊥AO，∴AO⊥面BCD，

∴BM是AB在面BCD内的射影，这样∠ABM是AB与平面BCD所成的角.

在△ABC中，AB=3，AC=2，∠BAC=60°，.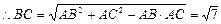 

在△ACD中， AC=AD=2，∠CAD=60°，∴△ACD是正三角形，AM=.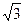

在Rt△BCM中，BC=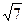，CM=1，

.
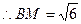