问题
解答题
平面内有12个点，其中有4个点共线，此外再无任何3点共线，以这些点为顶点，可得多少个不同的三角形？
答案
解：从12个点中任意取3个点有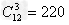
种取法，
而在共线的4个点中任意三点均不能构成三角形，
故不能构成三角形的情况有
种取法，
故这12个点构成三角形的个数为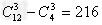
（个）。
搜题请搜索小程序“爱下问搜题”
平面内有12个点，其中有4个点共线，此外再无任何3点共线，以这些点为顶点，可得多少个不同的三角形？
解：从12个点中任意取3个点有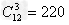种取法，
而在共线的4个点中任意三点均不能构成三角形，
故不能构成三角形的情况有种取法，
故这12个点构成三角形的个数为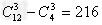（个）。