问题
选择题
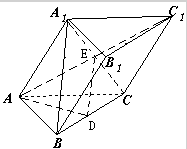
三棱柱ABC-A1B1
|
答案
连结A1C,交AC1于点E,取BC的中点D,连结AD、DE,
∵四边形AA1C1C是平行四边形,∴E是A1C的中点
∵D是BC的中点,∴DE是△A1BC的中位线,可得DE∥ .
A1B,1 2
因此,∠AED(或其补角)就是异面直线A1B与AC1所成的角.
设AB=AC=AA1=2,可得
∵∠A1AB=60°,
∴△A1AB是等边三角形,可得A1B=2,得DE=
A1B=1.1 2
同理,等边△A1AC中,中线AE=
A1A=3 2
,3
又∵∠BAC=90°,AB=AC=2,D为BC中点,
∴AD=
BC=1 2 1 2
=AB2+AC2 2
由此可得△ADE中,cos∠AED=
=AE2-ED2-AD2 2AE•ED
=3+1-2 2×
×13
.3 3
即异面直线A1B与AC1所成角的余弦值为
.3 3
故答案为:3 3