解：（1）∵小球的大小完全相同，三个盒子也完全相同，

∴把7个小球分成三份，比如分成3个、2个、2个这样三份放入三个盒子中，不论哪一份小球放人哪一个盒子均是同一种放法，

因此，只需将7个小球分成如下三份即可，即（7，0，0）、（6，1，0）、（5，2，0）、（5，1，1）、（4，3，0）、（4，2，1）、（3，3，1）、（3，2，2），

共有8种不同的放置方法；

（2）设三个盒子中小球的个数分别为x₁，x₂，x₃，显然有：x₁+x₂+x₃=7，

于是，问题就转化为求这个不定方程的非负整数解，

若令y_i=x_i+1 （i=1，2，3），由y₁+y₂+y₃=10 ，

问题又成为求不定方程y₁+y₂+y₃=10 的正整数解的组数的问题，

在10个球中间9个空档中，任取两个空档插入挡板，即可将10个球分成三组，

∴不定方程的解有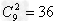组。