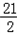问题
解答题
附加题：
（1）已知x﹣y=2+a，y﹣z=2﹣a，且a2=7，试求x2+y2+z2﹣xy﹣yz﹣zx的值．
（2）已知对多项式2x3﹣x2﹣13x+k进行因式分解时有一个因式是2x+3，试求4k2+4k+1的值．
答案
解：（1）∵x﹣y=2+a，y﹣z=2﹣a，
∴x﹣z=4，
∴（x﹣y）2+（y﹣z）2+（x﹣z）2=（2+a）2+（2﹣a）2+42，
即x2﹣2xy+y2+y2﹣2yz+z2+x2﹣2xz+z2=4+4a+a2+4﹣4a+a2+16，
整理得，2（x2+y2+z2﹣xy﹣yz﹣zx）=2（a2+12），
∵a2=7，
∴x2+y2+z2﹣xy﹣yz﹣zx=7+12=19；
（2）设因式分解的另一个因式为x2+ax+b，
则（2x+3）（x2+ax+b）
=2x3+2ax2+2bx+3x2+3ax+3b
=2x3+（2a+3）x2+（2b+3a）x+3b
=2x3﹣x2﹣13x+k，
所以
，
解得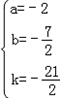
，
4k2+4k+1=（2k+1）2=[2×（﹣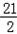
）+1]2=（﹣20）2=400．