如图,板长为L、间距为d的平行金属板水平放置,两板间所加电压大小为U,足够大光屏PQ与板的右端相距为a,且与板垂直。一带正电的粒子以初速度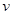 0沿两板间的中心线射入,射出电场时粒子速度的偏转角为37°。已知sin37°=0.6,cos37°=0.8,不计粒子的重力。
0沿两板间的中心线射入,射出电场时粒子速度的偏转角为37°。已知sin37°=0.6,cos37°=0.8,不计粒子的重力。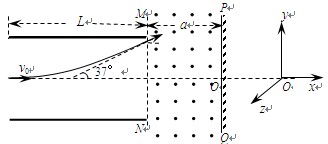
⑴求粒子的比荷q/m;
⑵若在两板右侧MN、光屏PQ间加如图所示的匀强磁场,要使粒子不打在光屏上,求磁场的磁感应强度大小B的取值范围;
⑶若在两板右侧MN、光屏PQ间仅加电场强度大小为E0、方向垂直纸面向外的匀强电场。设初速度方向所在的直线与光屏交点为O点,取O点为坐标原点,水平向右为x正方向,垂直纸面向外为z轴的正方向,建立如图所示的坐标系,求粒子打在光屏上的坐标(x,y,z)。
(1)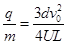 (2)
(2)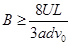 (3)(0,
(3)(0,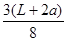 ,
,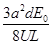 )
)
题目分析:⑴设粒子射出电场时速度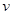 的水平分量为
的水平分量为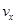 、竖直分量为
、竖直分量为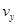
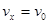 (1分)
(1分)
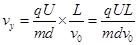 (1分)
(1分)
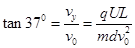 (2分)
(2分)
解得: 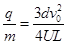 (1分)
(1分)
⑵设磁场的磁感应强度为B时粒子不能打在光屏上
由几何知识 有 (2分)
(2分)
由牛顿第二定律 有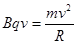 (1分)
(1分)
解得 磁感应强度大小范围: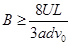 (2分)
(2分)
⑶ 粒子从两板间以速度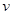 射出后作匀变速曲线运动,沿x、y轴方向均作匀速直线运动,沿z轴方向作初速度为零的匀加速直线运动。由题意知:
射出后作匀变速曲线运动,沿x、y轴方向均作匀速直线运动,沿z轴方向作初速度为零的匀加速直线运动。由题意知:
坐标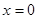 (1分)
(1分)
坐标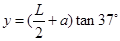 =
=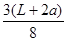 (2分)
(2分)
时间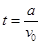 (1分)
(1分)
坐标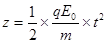 (1分)
(1分)
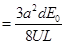 (1分)
(1分)
则粒子打在光屏上的坐标为(0,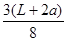 ,
,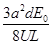 )
)
点评:粒子从两板间以速度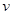 射出后作匀变速曲线运动,沿x、y轴方向均作匀速直线运动,沿z轴方向作初速度为零的匀加速直线运动。
射出后作匀变速曲线运动,沿x、y轴方向均作匀速直线运动,沿z轴方向作初速度为零的匀加速直线运动。