分别以CA、CC₁、CB为x轴、y轴和z轴建立如图坐标系，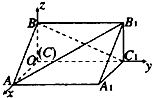

∵CA=CC₁=2CB，∴可设CB=1，CA=CC₁=2

∴A（2，0，0），B（0，0，1），B₁（0，2，1），C₁（0，2，0）

∴

BC1

=（0，2，-1），

AB1

=（-2，2，1）

可得

BC1

•

AB1

=0×（-2）+2×2+（-1）×1=-3，且|

BC1

|=

5

，|

AB1

|=3，

向量

BC1

与

AB1

所成的角（或其补角）就是直线BC₁与直线AB₁夹角，

设直线BC₁与直线AB₁夹角为θ，则cosθ=

BC1 • AB1

| BC1 || AB1 |

=

5

5

故答案为：

5

5