问题
填空题
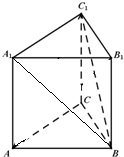
已知三棱柱ABC-A1B1C1的各条棱长都相等,且CC1⊥底面ABC,则异面直线BC1与AC所成角的余弦值为______.
答案
连接A1B,设该三棱柱的棱长为1,
∵三棱柱ABC-A1B1C1中,AC∥A1C1
∴∠A1C1B(或其补角)就是异面直线BC1与AC所成的角
∵CC1⊥底面ABC,
∴三棱柱ABC-A1B1C1是直三棱柱,可得四边形B1C1CB是矩形
∵BC=CC1=1,∴BC1=
,同理可得A1B=2 2
△A1C1B中,由余弦定理得:cos∠A1C1B=
=1+2-2 2×1× 2 2 4
即异面直线BC1与AC所成角的余弦值为2 4
故答案为:2 4