问题
解答题
（本小题满分15分）已知矩形纸片ABCD中，AB＝6cm，AD＝12cm，将矩形
纸片的右下角折起，使得该角的顶点B落在矩形的边AD上，且折痕MN的
端点M, N分别位于边AB, BC上，设∠MNB＝θ，sinθ＝t，MN长度为l．
（1）试将l表示为t的函数l＝f (t)；
（2）求l的最小值．
答案
(1) f (t)＝
(2)
解：(1) 设将矩形纸片的右下角折起后, 顶点B落在边AD上的B/处，则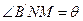
, 
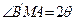
从而有：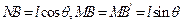
，
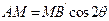
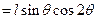． （3分）
∵
，∴
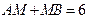，得：
l＝＝＝， 即f (t)＝ （7分）
(2) 
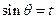, 0＜θ＜, 则0＜t＜, 设 
，
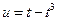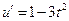，令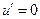
，得t＝ （9分）
当0＜t＜时，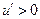
，当＜t＜时，
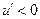， （12分）
所以当t＝时，
取到最大值：－·＝ （14分）
的最小值为＝ cm （15分）