问题
计算题
如图所示，水平放置的M、N两平行板相距为d=0.50m，板长为L=1m，，两板间有向下的匀强电场，场强E=300.0N/C，紧靠平行板右侧边缘的 xoy直角坐标系以N板右端为原点，在xoy坐标系的第一象限内有垂直纸面向外的匀强磁场，磁感强度B=
×10-2T，磁场边界OA与x轴夹角∠AOx=60°，现有比荷为
×106C/kg的带电粒子（重力不计），沿靠近M板的水平线垂直电场方向进入电场，离开电场后垂直于OA边界进入磁场区域，
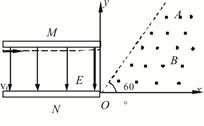
求：（1）带电粒子进入电场时的初速度v0；（2）带电粒子从进入电场到离开磁场的总时间。
答案
(1) 
(2) 
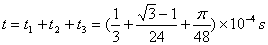
题目分析：（1）带电粒子要垂直射入磁场，则速度偏向角为30°
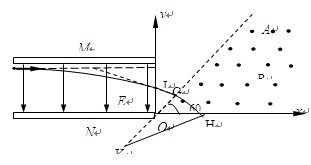
有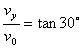
（2分）
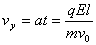（1分）
（1分）
（2）粒子在电场中的运动时间为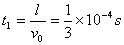 
（1分）
粒子在电场中的偏转距离为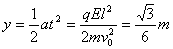
（1分）
粒子离开电场的速度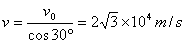
（1分）
粒子离开电场后做匀速直线运动，直线运动距离
（2分）
运动时间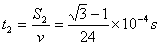
（1分）
粒子进入磁场后的轨道半径为R，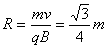
（2分）
由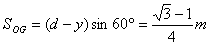
（2分）由正弦定理有
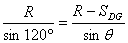
得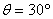
（2分）由此可知，带电粒子在磁场中的偏转角度为30°
由在磁场中的运动时间为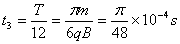
（2分）
则总运动时间为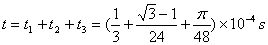
（2分）
点评：带电粒子在电场中运动时关键是对其受力分析，根据牛顿第二定律解题，在磁场中运动时，需要画轨迹，定圆心，求半径，