有9名学生,其中2名会下象棋但不会下围棋,3名会下围棋但不会下象棋,4名既会下围棋又会下象棋;现在要从这9名学生中选出2名学生,一名参加象棋比赛,另一名参加围棋比赛,共有多少种不同的选派方法?
设2名会下象棋但不会下围棋的同学组成集合A,3名会下围棋但不会下象棋的同学组成集合B,
4名既会下围棋又会下象棋的同学组成集合C,则选派2名参赛同学的方法可以分为以下4类:
第一类:A中选1人参加象棋比赛,B中选1人参加围棋比赛,方法数为
?C 12
=6种;C 13
第二类:C中选1人参加象棋比赛,B中选1人参加围棋比赛,方法数为
?C 14
=12种;C 13
第三类:C中选1人参加围棋比赛,A中选1人参加象棋比赛,方法数为
?C 14
=8种;C 12
第四类:C中选2人分别参加两项比赛,方法数为
=12种;A 24
由分类加法计数原理,选派方法数共有:6+12+8+12=38种.

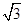 m/s平抛救生圈,第一个刚落到快艇,接着抛第二个,结果第二个救生圈刚好与甲队员同时抵达快艇,若人的质量m,重力加速度g=10 m/s2,(已知18×18=324, sin30°=0.5,cos30°=
m/s平抛救生圈,第一个刚落到快艇,接着抛第二个,结果第二个救生圈刚好与甲队员同时抵达快艇,若人的质量m,重力加速度g=10 m/s2,(已知18×18=324, sin30°=0.5,cos30°=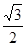 )问:
)问: