问题
填空题
将正方形ABCD沿对角线BD折成直二面角,给出下列四个结论:①AC⊥BD;②AB与CD所成角为60°;③△ACD为正三角形;④AB与平面BCD所成角为60°.其中正确的结论是______(填写结论的序号).
答案
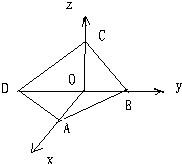
连接AC与BD交于O点,对折后如图所示,令OC=1
则O(0,0,0),A(1,0,0),B(0,1,0),C(0,0,1),D(0,-1,0)
则
=(-1,0,1),AC
=(0,-2,0),∵BD
•AC
=0,故①AC⊥BD正确;BD
=(-1,1,0),AB
=(0,-1,-1),则|cos<CD
,AB
>|=|CD
|=
•AB CD |
|•|AB
|CD
,故②AB与CD所成角为60°正确;1 2
∵|
|=|AC
|=|AD
|=CD
,∴③△ACD为正三角形正确;2
∵
为平面BCD的一个法向量,根据正方形的性质,易得AB与平面BCD所成角为45°,故④错误;OA
故答案为:①②③