问题
计算题
如图，在光滑水平长直轨道上有A、B两个绝缘体，它们之间有一根长L的轻质细线相连接，其中A的质量为m，B的质量为M=2m，A为带有电量为+q的物体，B不带电，空间存在着方向水平向右的匀强电场，电场强度为E。开始时用外力把A与B靠在一起并保持静止，某时刻撤去外力，A开始向右运动，直到细线绷紧，当细线被绷紧时，细线存在极短时间的弹力，而后B开始运动，已知B开始运动时的速度等于线刚绷紧前瞬间A的速度的1/2，设整个过程中，A的电荷量保持不变，求：
（1）B开始运动时，A运动的速度；
（2）通过计算来判断细线在第二次绷紧前A、B是否发生碰撞；
（3）在（2）中，若A、B发生碰撞，求碰撞前瞬间B的位移；若A、B不发生碰撞，求细线第二次绷紧前瞬间B的位移。
答案
解：（1）从运动到拉直时，A的速度为v0，则：
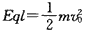，解得：
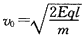
绷紧前后，系统动量守恒，mv0=mvA+2m·1/2v0
解得：vA=0
（2）第一次绷紧后，A作初速度为0的匀加速直线运动，B做0.5v0的匀速直线运动。现假设二者能碰撞，B追上A的时间为t，则须同时满足下面两个条件：
①二者能相遇，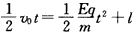
，且t有实数解
②相遇时后面速度比前面大，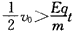
由①得到一元二次方程的判别式
，故t无实数解，说明B追不上A，也就没有②式成立，所以，二者不会发生碰撞
（3）设第二次绷紧时间为t2，则有：
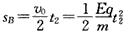
解得：