如图15所示，水平绝缘轨道AB与处于竖直平面内的半圆形绝缘光滑轨道BC平滑连接，半圆形轨道的半径R=0.40m。轨道所在空间存在水平向右的匀强电场，电场强度E=1.0×104 N/C。现有一电荷量q=+1.0×10-4C，质量m=0.10 kg的带电体（可视为质点），在水平轨道上的P点由静止释放，带电体运动到圆形轨道最低点B时的速度vB=5.0m/s。已知带电体与水平轨道间的动摩擦因数μ=0.50，重力加速度g=10m/s2。求：
（1）带电体运动到圆形轨道的最低点B时，圆形轨道对带电体支持力的大小；
（2）带电体在水平轨道上的释放点P到B点的距离；
（3）带电体第一次经过C点后，落在水平轨道上的位置到B点的距离。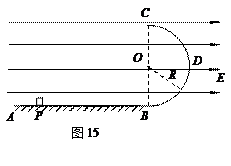
（1）7.25 N（2）2.5 m（3）0.40m
（1）设带电体在B点受到的支持力为FN，依据牛顿第二定律
FN-mg=m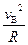
.................................................3分
解得FN="7.25" N…..................................................2分
（2）设PB间的距离为s，依据动能定理
(qE-mmg)s=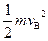
……..…............................ ........3分
解得s="2.5" m ……..….. .............................….........…2分
（3）设带电体运动到C点的速度为vC，依据机械能守恒定律
=
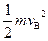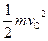+2mgR........................…………….…….….…...…1分
带电体离开C点后在竖直方向上做自由落体运动，设在空间运动的时间为t
2R=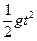
.................................................1分
在水平方向上做匀减速运动，设在水平方向的加速度大小为a，依据牛顿第二定律
qE=ma................................... 1分
设落在水平轨道上的位置到B点的距离为x，依据运动学公式
x=vct-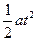
..................................1分
解得 x=0.40m.................................. 2分