问题
填空题
某商场销售一批羊毛衫，每天可售出20件，每件盈利50元，据市场分析，如果一件羊毛
衫每降价1元，每天可多售出2件，针对这种销售情况，每件羊毛衫降价 元
时，商场一天销售这种羊毛衫的盈利达到最大.
答案
20
每件羊毛衫降价x元，商场每天销售这种羊毛衫的盈利为y，则每件羊毛衫的利润为（50-x）元，销售量为（20+2x）件，则每天的利润y=（50-x）（20+2x），整理得到y=-2x2+80x+1000，然后利用二次函数的最值问题进行解决．
解：每件羊毛衫降价x元，商场每天销售这种羊毛衫的盈利为y，
根据题意得y=（50-x）（20+2x）
=-2x2+80x+1000，
∵a=-2＜0，
∴当x=-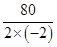
=20时，y有最大值，
即每件羊毛衫降价20元时，商场一天销售这种羊毛衫的盈利达到最大．
故答案为20．
考查了二次函数的最值问题：二次函数y=ax2+bx+c（a≠0）的图象为抛物线，对称轴为直线x=-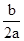
，当a＞0，抛物线开口向上，y有最小值 
，y随x的增大而减小；当a＜0，抛物线开口向下，y有最大值 ，y随x的增大而增大．