问题
解答题
(本题满分12分)
已知函数f(x)=ax3+bx+c (a>0)为奇函数,其图象在点(1,f(1))处的切线与直线x-6y-7=0垂直,导数f/(x)的 最小值为-12,求a,b,c的值.
答案
a="2," b="-12, " C=0.
解:由x-6x-7=0得,k=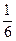
∵f(x)=ax3+bx+c, ∴f/(x)=3ax2+b ∴f/(1)="3a+b=-6 "
又当x=0时,f/(x)min=b=-12,∴a=2
∵f(x)为奇函数,∴f(0)=0,∴c=0
∴a="2," b="-12, " C=0.
